2023年高考数学模拟试卷01(浙江省)(原卷版)
![]()
![]()
![]()
![]()
![]()
![]() 2023年高考数学模拟试卷01(浙江省)
2023年高考数学模拟试卷01(浙江省)
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.![]() )
)
1.(2022·吕梁模拟)已知集合A={x|x2-2x-3<0},B={x|log2x<2},则A∩B等于( )
A.(-1,4) B.(-1,3)
C.(0,3) D.(0,4)
2.(2022·长春模拟)已知复数z的共轭复数=,则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.(2022·重庆调研)函数y=ln cos x的图象是( )
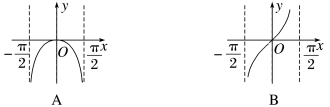
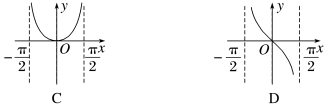
4.(2022·郑州模拟)如图,在五面体ABCDEF中,四边形ABCD是正方形,AB=4,EF=2,△BCF,△ADE都是等边三角形,则五面体ABCDEF的体积为( )
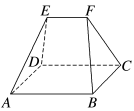
A. B.
C. D.4
5.函数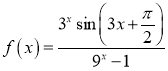 图像大致为( )
图像大致为( )
A.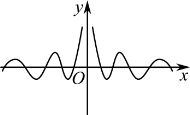 B.
B.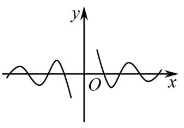
C. D.
D.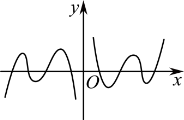
6.如图,在△ABC中,M为线段BC的中点,G为线段AM上一点且![]() ,过点G的直线分别交直线AB、AC于P、Q两点,
,过点G的直线分别交直线AB、AC于P、Q两点,![]() ,
,![]() ,则
,则![]() 的最小值为( )
的最小值为( )
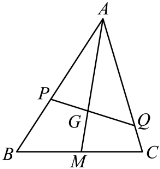
A.![]() B.1 C.
B.1 C.![]() D.4
D.4
7.已知椭圆![]() 的右焦点为F,以椭圆
的右焦点为F,以椭圆![]() 的长轴为直径作圆
的长轴为直径作圆![]() ,过点F作不与坐标轴垂直的两条直线
,过点F作不与坐标轴垂直的两条直线![]() ,
,![]() ,其中
,其中![]() 与椭圆
与椭圆![]() 交于M,N两点,
交于M,N两点,![]() 与圆
与圆![]() 交于P,Q两点,若
交于P,Q两点,若![]() ,且都有
,且都有![]() ,则实数
,则实数![]() 的取值范围为( ).
的取值范围为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
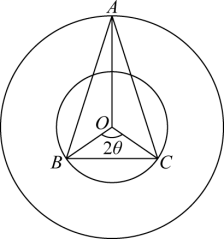
8.某单位科技活动纪念章的结构如图所示,![]() 是半径分别为
是半径分别为![]() 的两个同心圆的圆心,等腰三角形
的两个同心圆的圆心,等腰三角形![]() 的顶点
的顶点![]() 在外圆上,底边
在外圆上,底边![]() 的两个端点都在内圆上,点
的两个端点都在内圆上,点![]() 在直线
在直线![]() 的同侧.若线段
的同侧.若线段![]() 与劣弧
与劣弧![]() 所围成的弓形面积为
所围成的弓形面积为![]() ,△
,△![]() 与△
与△![]() 的面积之和为
的面积之和为![]() ,设
,设![]() .经研究发现当
.经研究发现当![]() 的值最大时,纪念章最美观,当纪念章最美观时,
的值最大时,纪念章最美观,当纪念章最美观时,![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.![]() )
)
9.已知![]() ,
,![]() 均为复数,则下列结论中正确的有( )
均为复数,则下列结论中正确的有( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]() 是实数
是实数
C.![]() D.若
D.若![]() ,则
,则![]() 是实数
是实数
10.有![]() 个相同的球,分别标有数字
个相同的球,分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从中有放回的随机取两次,每次取
,从中有放回的随机取两次,每次取![]() 个球.记第一次取出的球的数字为
个球.记第一次取出的球的数字为![]() ,第二次取出的球的数字为
,第二次取出的球的数字为![]() .设
.设![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() ,则( )
,则( )
A.![]()
B.![]()
C.事件“![]() ”与“
”与“![]() ”互斥
”互斥
D.事件“![]() ”与“
”与“![]() ”对立
”对立
11.取名于荷兰数学家鲁伊兹·布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理.该定理表明:对于满足一定条件的图象连续不间断的函数![]() ,在其定义域内存在一点
,在其定义域内存在一点![]() ,使得
,使得![]() ,则称
,则称![]() 为函数
为函数![]() 的一个不动点,那么下列函数具有“不动点”的是( )
的一个不动点,那么下列函数具有“不动点”的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
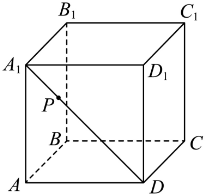
12.如图,正方体![]() 棱长为
棱长为![]() ,
,![]() 是直线
是直线![]() 上的一个动点,则下列结论中正确的是( )
上的一个动点,则下列结论中正确的是( )
A.![]() 的最小值为
的最小值为![]()
B.![]() 的最小值为
的最小值为![]()
C.三棱锥![]() 的体积不变
的体积不变
D.以点![]() 为球心,
为球心,![]() 为半径的球面与面
为半径的球面与面![]() 的交线长
的交线长![]()
三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)
13.已知平面向量a,b满足a=(1,2),|b|=,a·b=,则cos〈a,b〉=________.
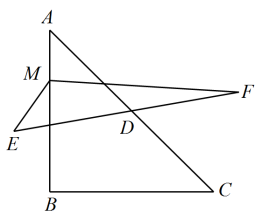
14.如图,在等腰直角![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,将线段
的中点,将线段![]() 绕点
绕点![]() 旋转得到线段
旋转得到线段![]() .设
.设![]() 为线段
为线段![]() 上的点,则
上的点,则![]() 的最小值为___________.
的最小值为___________.
15.在线投标问题的定义是:商家给出一个足够大的正整数M,但投标者不知道M的值,故只能通过不断给出价格序列![]() 来竞标,已知
来竞标,已知![]() ,
,![]() .若正整数k使得
.若正整数k使得![]() ,则此次竞标投标者共花费
,则此次竞标投标者共花费![]() 中标,我们的目标是对于任意足够大的正整数M,最小化竞争比
中标,我们的目标是对于任意足够大的正整数M,最小化竞争比![]() ,则当
,则当![]() ________.时,在线投标问题的竞争比最小.
________.时,在线投标问题的竞争比最小.
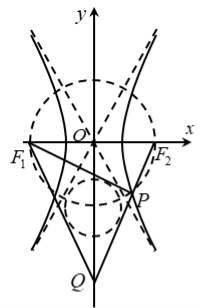
16.已知![]() 为双曲线
为双曲线![]() 的左右焦点,过点
的左右焦点,过点![]() 作一条渐近线的垂线交双曲线右支于点P,直线
作一条渐近线的垂线交双曲线右支于点P,直线![]() 与y轴交于点Q(P,Q在x轴同侧),连接
与y轴交于点Q(P,Q在x轴同侧),连接![]() ,如图,若
,如图,若![]() 内切圆圆心恰好落在以
内切圆圆心恰好落在以![]() 为直径的圆上,则
为直径的圆上,则![]() ________;双曲线的离心率
________;双曲线的离心率![]() ________.
________.
四、解答题(本题共6小题,共70分,其中第16题10分,其它每题12分,解答应写出文字说明、证明过程或演算步骤.![]() )
)
17.设函数![]() ,数列
,数列![]() 满足
满足![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
18.(12分)(2022·新余模拟)如图,在三棱锥P-ABC中,已知PA=PB=PC=AB=AC,E是PA的中点.
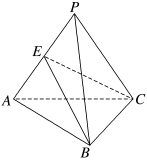
(1)求证:平面PAB⊥平面BCE;
(2)若BC=AB,求平面ABC与平面ABE夹角的正弦值.
19.在钝角![]() 中,内角
中,内角![]() ,
,![]() ,
,![]() 的对边为
的对边为![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)求![]() 的取值范围.
的取值范围.
20.京东配送机器人是由京东研发,进行快递包裹配送的人工智能机器人.![]() 年
年![]() 月
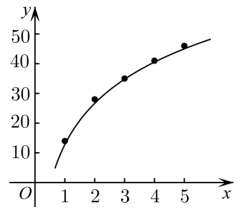
月![]() 日,京东配送机器人在中国人民大学顺利完成全球首单配送任务,作为整个物流系统中末端配送的最后一环,配送机器人所具备的高负荷、全天候工作、智能等优点,将为物流行业的“最后一公里”带去全新的解决方案.已知某市区
日,京东配送机器人在中国人民大学顺利完成全球首单配送任务,作为整个物流系统中末端配送的最后一环,配送机器人所具备的高负荷、全天候工作、智能等优点,将为物流行业的“最后一公里”带去全新的解决方案.已知某市区![]() 年
年![]() 到
到![]() 月的京东快递机器人配送的比率图如图所示,对应数据如下表所示:
月的京东快递机器人配送的比率图如图所示,对应数据如下表所示:
|
|
|
|
|
|
时间代码 |
|
|
|
|
|
配送比率 |
|
|
|
|
|
(1)如果用回归方程![]() 进行模拟,请利用以下数据与公式,计算回归方程;
进行模拟,请利用以下数据与公式,计算回归方程;
![]() ,
,![]() ,
,![]() .
.
参考公式:若![]() ,则
,则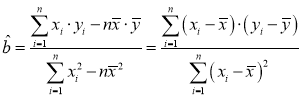
(2)已知某收件人一天内收到![]() 件快递,其中京东快递
件快递,其中京东快递![]() 件,菜鸟包裹
件,菜鸟包裹![]() 件,邮政快递
件,邮政快递![]() 件,现从这些快递中任取
件,现从这些快递中任取![]() 件,
件,![]() 表示这四件快递里属于京东快递的件数,求随机变量
表示这四件快递里属于京东快递的件数,求随机变量![]() 的分布列以及随机变量
的分布列以及随机变量![]() 的数学期望.
的数学期望.
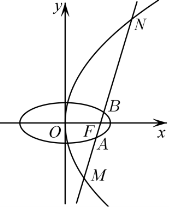
21.已知抛物线G:![]() 的焦点与圆E:
的焦点与圆E:![]() 的右焦点F重合,椭圆E的短轴长为2.
的右焦点F重合,椭圆E的短轴长为2.
(1)求椭圆E的方程;
(2)过点F且斜率为k的直线l交椭圆E于A、B两点,交抛物线G于M,N两点,请问是否存在实常数t,使![]() 为定值?若存在,求出t的值;若不存在,说明理由.
为定值?若存在,求出t的值;若不存在,说明理由.
22.)(2022·潍坊模拟)已知函数f(x)=ex-ax-a,a∈R.
(1)讨论f(x)的单调区间;
(2)当a=1时,令g(x)=.
①证明:当x>0时,g(x)>1;
②若数列{xn}(n∈N*)满足x1=,![]() =g(xn),证明:2n(
=g(xn),证明:2n(![]() -1)<1.
-1)<1.
![]()
![]() 学科网(北京)股份有限公司
学科网(北京)股份有限公司
![]()
![]() 学科网(北京)股份有限公司
学科网(北京)股份有限公司




