切割线定理怎么证明
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。切割线定理的推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
切割线定理的证明
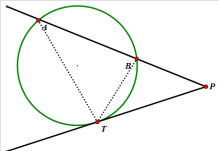
设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT²=PA·PB。
证明:连接AT, BT。
∵ ∠PTB=∠PAT(弦切角定理);∠APT=∠TPB(公共角);
∴ △PBT∽△PTA(两角对应相等,两三角形相似);
∴PB:PT=PT:AP;
即:PT²=PB·PA。
割线定理
割线定理,指的是从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。割线定理为圆幂定理之一。
文字表达:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
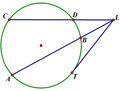
数学语言:从圆外一点L引两条割线与圆分别交于A.B.C.D 则有 LA·LB=LC·LD=LT²。
几何语言:∵割线LDC和LBA交于圆O于ABCD点
∴LA·LB=LC·LD=LT²
如图所示。(LT为切线)