高等数学常用不定积分公式
在微积分中,一个函数f 的不定积分,或原函数,或反导数,是一个导数等于f的函数 F ,即F′= f。不定积分和定积分间的关系由微积分基本定理确定。其中F是f的不定积分。
不定积分公式有哪些


积分公式种类
不定积分
设 是函数f(x)的一个原函数,我们把函数f(x)的所有原函数F(x)+C(C为任意常数)叫做函数f(x)的不定积分,记作,即∫f(x)dx=F(x)+C.其中∫叫做积分号,f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式,C叫做积分常数,求已知函数不定积分的过程叫做对这个函数进行积分。
注:∫f(x)dx+c1=∫f(x)dx+c2, 不能推出c1=c2
定积分
积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说,对于一个给定的实函数f(x),在区间[a,b]上的定积分记为:
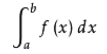
若f(x)在[a,b]上恒为正,可以将定积分理解为在Oxy坐标平面上,由曲线(x,f(x))、直线x=a、x=b以及x轴围成的面积值(一种确定的实数值)。
其他
积分的种类还有如下几类:
黎曼积分
达布积分
勒贝格积分
黎曼-斯蒂尔杰斯积分
数值积分
